Introduction
ICS 40: Compiler Design Principles
This subject is an introduction to the design and implementation of high-level programming language translators and compilers. It will open with a discussion of translators related to compilers, followed by an overview of the phases and data structures involved in compilation. Topics including lexical analysis, parsing techniques, symbol tables, run-time storage allocation, semantic routines, code generation, and optimization will then be covered with a series of projects assigned to illustrate practical issues.
Tuesday, July 29, 2008
Translation Rules
Infix to Prefix
1. If E is a variable or constant then Prefix(E) = E
2. If E is E1 op E2 then Prefix(E) = Prefix(E1 op E2) = op Prefix(E1) Prefix(E2)
3. If E is (E1) then Prefix(E) = Prefix(E1)
Example:
Prefix( ( 9 – 5 ) + 2 )
= + Prefix(( 9 - 5 )) Prefix(2)
= + Prefix( 9 - 5 ) Prefix(2)
= + - Prefix(9) Prefix(5) Prefix(2)
= + - 9 5 2
Postfix to Infix
1. If E is a variable or constant then Infix(E) = E
2. If E is E1 E2 op then Infix(E) = Infix(E1 op E2) = Infix(E1) op Infix(E2)
3. If E is (E1) then Infix(E) = Infix(E1)
Example:
Infix( ( 9 5 – ) 2 + )
= ( Infix(9) - Infix(5) ) + Infix(2)
= ( 9 - 5 ) + 2
Postfix to Prefix
1. If E is a variable or constant then Prefix(E) = E
2. If E is E1 E2 op then Prefix(E) = Prefix(E1 op E2) = op Prefix(E1) Prefix(E2)
3. If E is (E1) then Prefix(E) = Prefix(E1)
Example:
Prefix( 9 5 – 2 + )
= + Prefix( 9 5 ) - Prefix(2)
= + - Prefix(9) Prefix(5) Prefix(2)
= + - 9 5 2
Tuesday, July 22, 2008
Chapter 2 Exercises
2.1 Consider the context free grammar
S → SS+ | SS* | a
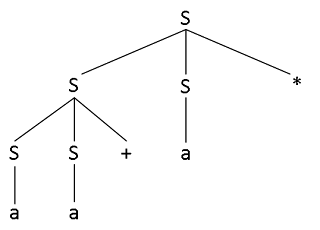
a) Show how the string aa+a* can be generated by this grammar.
S → SS*
→ SS+S*
→ aS+S*
→ aa+S*
→ aa+a*
b) Construct a parse tree for this string.
c) What language is generated by this grammar? Justify your answer.
This grammar generates a language that consists of any possible arithmetic operations involving a with the use of only the + and * operations and the postfix notation. The only non-terminal symbol in the grammar is a and it replaces all occurrences of S, leaving only a statement consisting of a series of a's and the + and * operations.
2.2 What language is generated by the following grammars?
a) S → 0S1 | 01
This grammar generates a language consisting of a series of 0's and 1's coming between a 0 and a 1. There are to be at least two 0's and two 1's and there are the same number of 0's as 1's.
b) S → +SS | -SS | a
This grammar generates a language that consists of any possible arithmetic operations involving a with the use of only the + and * operations and the prefix notation.
c) S → S (S) S |
This grammar generates a language that consists of a series of adjacent and nested, matched pairs of parentheses.
d) S → a S b S | b S a S | ε
This grammar generates a language that consists of equal number of a's and b's in no particular order.
e) S → a | S + S | S S | S * | ( S )
This grammar generates a language that consists of any possible arithmetic operations involving a with the use of only the + and * operations and sets of matched parentheses. It may involve both postfix and infix notations.
2.3 Which of the grammars in Exercise 2.2 are ambiguous?
Letter e in Exercise 2.2 is ambiguous. The string a+a* can be parsed in more than one way:
a)
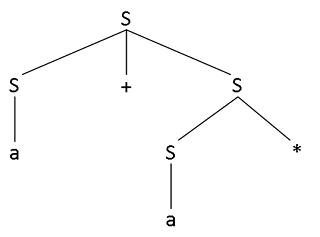
b)

2.4 Construct unambiguous context-free grammars for each of the following languages.
a) Arithmetic expressions in postfix notation.
expr → expr expr +
expr → expr expr -
expr → digit
digit → 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
b) Left-associative lists of identifiers separated by commas.
expr → expr, id
expr → id
c) Right-associative lists of identifiers separated by commas.
expr → id, expr
expr → id
d) Arithmetic expressions of integers and identifiers with the four binary operators + , - , * , /.
expr → expr + term | expr - term | term
term → term * factor | term / factor | factor
factor → digit | id | (expr)
e) Add unary plus and minus to the arithmetic operators of (d).
expr → expr + term | expr - term | term
term → term * factor | term / factor | factor
factor → digit | id | (expr) | +factor | -factor
S → SS+ | SS* | a
a) Show how the string aa+a* can be generated by this grammar.
S → SS*
→ SS+S*
→ aS+S*
→ aa+S*
→ aa+a*
b) Construct a parse tree for this string.

c) What language is generated by this grammar? Justify your answer.
This grammar generates a language that consists of any possible arithmetic operations involving a with the use of only the + and * operations and the postfix notation. The only non-terminal symbol in the grammar is a and it replaces all occurrences of S, leaving only a statement consisting of a series of a's and the + and * operations.
2.2 What language is generated by the following grammars?
a) S → 0S1 | 01
This grammar generates a language consisting of a series of 0's and 1's coming between a 0 and a 1. There are to be at least two 0's and two 1's and there are the same number of 0's as 1's.
b) S → +SS | -SS | a
This grammar generates a language that consists of any possible arithmetic operations involving a with the use of only the + and * operations and the prefix notation.
c) S → S (S) S |
This grammar generates a language that consists of a series of adjacent and nested, matched pairs of parentheses.
d) S → a S b S | b S a S | ε
This grammar generates a language that consists of equal number of a's and b's in no particular order.
e) S → a | S + S | S S | S * | ( S )
This grammar generates a language that consists of any possible arithmetic operations involving a with the use of only the + and * operations and sets of matched parentheses. It may involve both postfix and infix notations.
2.3 Which of the grammars in Exercise 2.2 are ambiguous?
Letter e in Exercise 2.2 is ambiguous. The string a+a* can be parsed in more than one way:
a)

b)

2.4 Construct unambiguous context-free grammars for each of the following languages.
a) Arithmetic expressions in postfix notation.
expr → expr expr +
expr → expr expr -
expr → digit
digit → 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
b) Left-associative lists of identifiers separated by commas.
expr → expr, id
expr → id
c) Right-associative lists of identifiers separated by commas.
expr → id, expr
expr → id
d) Arithmetic expressions of integers and identifiers with the four binary operators + , - , * , /.
expr → expr + term | expr - term | term
term → term * factor | term / factor | factor
factor → digit | id | (expr)
e) Add unary plus and minus to the arithmetic operators of (d).
expr → expr + term | expr - term | term
term → term * factor | term / factor | factor
factor → digit | id | (expr) | +factor | -factor
Tuesday, June 24, 2008
Phases of a Compiler
A compiler is a computer program (or set of programs) that translates text written in a computer language (the source language) into another computer language (the target language). The original sequence is usually called the source code and the output called object code. Commonly the output has a form suitable for processing by other programs (e.g., a linker), but it may be a human-readable text file.[1] There are six (6) Phases of a Compiler and these are:
1. Lexical Analyzer
- converts a sequence of characters into a sequence of tokens. Programs performing lexical analysis are called lexical analyzers or lexers. A lexer is often organized as separate scanner and tokenizer functions, though the boundaries may not be clearly defined.[2]
2. Syntax Analyzer
- checks that something conforms to the rules of a given syntax and analysing its structure according to those rules.[3]
3. Semantic Analyzer
- checks the source program for semantic errors and gathers type information for the subsequent code-generation phase.[4]
4. Intermediate Code Generator
- is generated as a program for an abstract machine. It helps to easily translate into the target program. We consider the three-address code, similar to assembly.[5]
5. Code Optimizer
- attempts to improve the intermediate code, so that faster-running machine code will result.[6]
6. Code Generator
- is the process by which a compiler's code generator converts some internal representation of source code into a form (e.g., machine code) that can be readily executed by a machine (often a computer).[7]
References:
[1] http://en.wikipedia.org/wiki/Compiler
[2] http://en.wikipedia.org/wiki/Lexical_analysis
[3] http://www.cmis.brighton.ac.uk/~je/adacraft/glossary.htm
[4] http://http://www.cmis.brighton.ac.uk/~je/adacraft/glossary.htm
[5] http://www.inf.unibz.it/~artale/Compiler/slide1.pdf
[6] http://www.mec.ac.in/resources/notes/notes/compiler/Module1/intro.html
[7] http://en.wikipedia.org/wiki/Code_generation_(compiler)
[1] http://en.wikipedia.org/wiki/Compiler
[2] http://en.wikipedia.org/wiki/Lexical_analysis
[3] http://www.cmis.brighton.ac.uk/~je/adacraft/glossary.htm
[4] http://http://www.cmis.brighton.ac.uk/~je/adacraft/glossary.htm
[5] http://www.inf.unibz.it/~artale/Compiler/slide1.pdf
[6] http://www.mec.ac.in/resources/notes/notes/compiler/Module1/intro.html
[7] http://en.wikipedia.org/wiki/Code_generation_(compiler)
Subscribe to:
Comments (Atom)
