Chapter 2 Exercises

2.1 Consider the context free grammar

S → SS+ | SS* | a

a) Show how the string aa+a* can be generated by this grammar.

S → SS*
→ SS+S*
→ aS+S*
→ aa+S*
→ aa+a*

b) Construct a parse tree for this string.



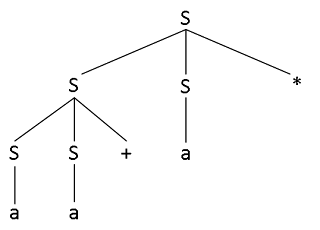
c) What language is generated by this grammar? Justify your answer.

This grammar generates a language that consists of any possible arithmetic operations involving a with the use of only the + and * operations and the postfix notation. The only non-terminal symbol in the grammar is a and it replaces all occurrences of S, leaving only a statement consisting of a series of a's and the + and * operations.

2.2 What language is generated by the following grammars?

a) S → 0S1 | 01

This grammar generates a language consisting of a series of 0's and 1's coming between a 0 and a 1. There are to be at least two 0's and two 1's and there are the same number of 0's as 1's.

b) S → +SS | -SS | a

This grammar generates a language that consists of any possible arithmetic operations involving a with the use of only the + and * operations and the prefix notation.

c) S → S (S) S | ε

This grammar generates a language that consists of a series of adjacent and nested, matched pairs of parentheses.

d) S → a S b S | b S a S | ε

This grammar generates a language that consists of equal number of a's and b's in no particular order.

e) S → a | S + S | S S | S * | ( S )

This grammar generates a language that consists of any possible arithmetic operations involving a with the use of only the + and * operations and sets of matched parentheses. It may involve both postfix and infix notations.

2.3 Which of the grammars in Exercise 2.2 are ambiguous?

Letter e in Exercise 2.2 is ambiguous. The string a+a* can be parsed in more than one way:

a)

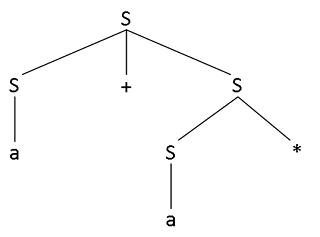
b)


2.4 Construct unambiguous context-free grammars for each of the following languages.

a) Arithmetic expressions in postfix notation.

expr → expr expr +
expr → expr expr -
expr → digit
digit → 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

b) Left-associative lists of identifiers separated by commas.

expr → expr, id
expr → id

c) Right-associative lists of identifiers separated by commas.

expr → id, expr
expr → id

d) Arithmetic expressions of integers and identifiers with the four binary operators + , - , * , /.

expr → expr + term | expr - term | term
term → term * factor | term / factor | factor
factor → digit | id | (expr)

e) Add unary plus and minus to the arithmetic operators of (d).

expr → expr + term | expr - term | term
term → term * factor | term / factor | factor
factor → digit | id | (expr) | +factor | -factor